Logarithms
A logarithm is the inverse of exponentiation. Math Is Fun has a nice intro to the topic. There is also Wikipedia, Khan Academy, etc.
Think of this question: “How many x’s multiply together to make y”? For example, “How many 2’s multiply together to make 8?” We multiply 2 three times to get 8.
-
\(2 * 2 * 2 = 8\)
-
\(log₂(8) = 3\)
Therefore, \(log₂(8) = 3\). Read as “log base 2 of 8 is 3” or “the base-2 log of 8 is 3”. In this example, 2 is the base, and 3 is the logarithm. 8 is the number we want to get by multiplying \(x\) \(n\) times.
-
\(log_{2}(n) = e\) such that \(2 \times e = n\).
-
\(log₂(8) = 3\) such that \(2³ = 8\).
|
For analyzing algorithms' time and space complexity, we mostly care about the general trend. We sometimes omit the base when informally speaking about algorithms that have logarithmic time and/or space complexity. We say “this algorithm is log of n”, actually meaning log base 2 of n (\(log_{2}(n)\)). |
|
A logarithm must have a base. That is, simply “log” is not a real (logarithmic) math operation. \(log_{2}\) or \(log_{8}\) are real logarithmic math operations. |
|
A loose definition is that \(log_{2}\) of a number roughly measures the number of times you can divide a number by 2 before you get a value that is less than or equal to \(1\). |
See this slide from Colt Steele for some visual clue on how good logarithmic time complexity fairs in comparison with some others:
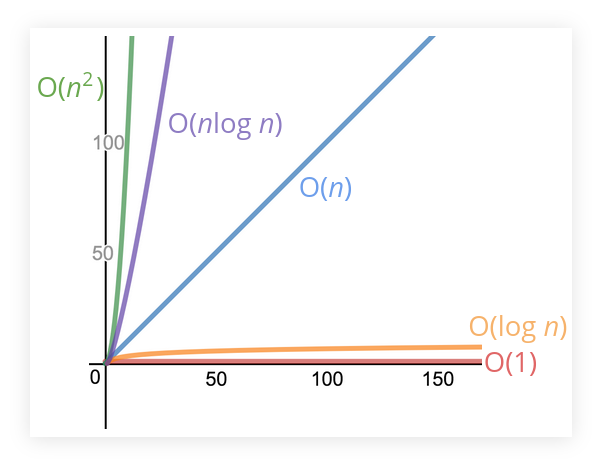
Types of algorithms that sometimes involves logarithmic time and/or space complexity:
-
Certain searching algorithms have logarithmic time complexity.
-
Sorting algorithms (especially some of the most efficient ones).
-
Recursive algorithms sometimes have logarithmic space complexity.