Sliding Window Examples
longestUniqSubSeq()
Problem: given a string the find the longest sequence of unique characters.
For instance, in "hellothere", "hel" is the first sequence of unique chars, because then "l" is repeated. Then, we start at the next "l" and the next unique sequence of chars is "lother".
h e l l o t h e r e
------- ----------------
/ \
/ \--> second sequence
v of unique chars
first sequence
of unique charsmaxSubArrSum()
Write a function which accepts an array of integers xs and an integer len and computes the maximum sum of len consecutive elements in xs.
Unit Tests
Unresolved include directive in modules/ROOT/pages/problem-solving-patterns/sliding-window-examples.adoc - include::example$src/05-problem-solving-patterns/maxSubArrSum.test.ts[]v1 nested loops
TIME COMPLEXITY: \(O(n^2)\) because there is a loop inside a loop.
SPACE COMPLEXITY: \(O(1)\) as no extra storage is required besides a few control variables to store numbers.
Unresolved include directive in modules/ROOT/pages/problem-solving-patterns/sliding-window-examples.adoc - include::example$src/05-problem-solving-patterns/maxSubArrSum-v1.ts[]| 1 | This is necessary as are always looking ahead so we avoid looking past the end of the input array. |
v2 sliding window approach
This solution is \(O(n)\) time complexity because only one loop is performed.
TIME COMPLEXITY: \(O(n)\) as it runs a single loop.
SPACE COMPLEXITY: \(O(1)\) as no extra space is required besides a few control variables that store numbers.
Unresolved include directive in modules/ROOT/pages/problem-solving-patterns/sliding-window-examples.adoc - include::example$src/05-problem-solving-patterns/maxSubArrSum-v2.ts[]| 1 | -Infinity because we need to take the into account the fact that the sum could be negative.
Starting with 0 would be a bad decision here. |
Consider this example:
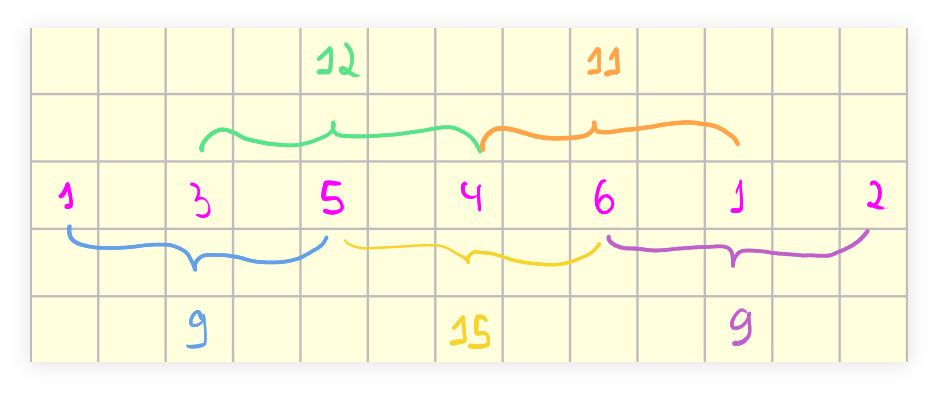
We keep looping the input array, sliding the window one element at at time, each time subtracting the left element of the previous window, and adding the new element that the window slides on to.
[1, 3, 5, 4, 6, 1, 2]
·······
- ······+
- ······+
- ······+
- ······+
9
9 - 1 + 4 → 12
12 - 3 + 6 → 15
15 - 5 + 1 → 11
11 - 4 + 2 → 9minSubArrLen()
Write a function called minSubArrLen which accepts two parameters: an array of positive integers and a positive integer.
This function should return the minimal length of a contiguous subarray of which the sum is greater than or equal to the integer passed to the function. If there isn’t one, return 0 instead.
Unit Tests
Unresolved include directive in modules/ROOT/pages/problem-solving-patterns/sliding-window-examples.adoc - include::example$src/05-problem-solving-patterns/minSubArrLen.test.ts[]v1 convoluted logic 😅
TIME COMPLEXITY: \(O(n²)\). (TODO: is it really \(O(n²)\)‽). The array is iterated only once, but also reduce to sum slides.
SPACE COMPLEXITY: \(O(1)\). Just a few control numeric variables are used.
Unresolved include directive in modules/ROOT/pages/problem-solving-patterns/sliding-window-examples.adoc - include::example$src/05-problem-solving-patterns/minSubArrLen-v1.ts[]This solution contains too many conditions and the logic is convoluted and hard to understand. The next solution (by Colt Steele) is much simpler and more elegant.
v2 simpler and elegant
TIME COMPLEXITY: \(O(n²)\).
SPACE COMPLEXITY: \(O(n)\).
Unresolved include directive in modules/ROOT/pages/problem-solving-patterns/sliding-window-examples.adoc - include::example$src/05-problem-solving-patterns/minSubArrLen-v2.ts[]| 1 | If current window doesn’t add up to the given sum then move the window to right. |
| 2 | If current window adds up to at least the sum given then the window can be shrank. |
| 3 | Current total less than required total but we reach the end. This is needed lest an infinite loop is created. |
This solution is much cleaner and elegant than the previous one. It uses less confusing conditions and updates variables in less places.
It sometimes cause minLen to be incorrect until some future iteration fixes it with a correct value that will work out in the end.
The same for sum, which sometimes gets back to less than the previous n value.
But it is brilliant that it simplifies logic, and in the end everything works out magnificently.
findLongestSubstr()
Write a function called findLongestSubstr, which accepts a string and returns the length of the longest substring with all distinct characters.
Unit Tests
Unresolved include directive in modules/ROOT/pages/problem-solving-patterns/sliding-window-examples.adoc - include::example$src/05-problem-solving-patterns/longestSubstr.test.ts[]v1 convoluted logic 😅
TIME COMPLEXITY: \(O(n)\) because the input is looped once.
SPACE COMPLEXITY: \(O(n)\) since seen chars are stored in an object which could potentially be as big as the input string.
Unresolved include directive in modules/ROOT/pages/problem-solving-patterns/sliding-window-examples.adoc - include::example$src/05-problem-solving-patterns/longestSubstr-v1.ts[]v2 more concise and elegant
TIME COMPLEXITY: \(O(n)\). The input is looped over once.
SPACE COMPLEXITY: \(O(n)\). Seen chars are stored in an object which could potentially be as big as the input string.
Unresolved include directive in modules/ROOT/pages/problem-solving-patterns/sliding-window-examples.adoc - include::example$src/05-problem-solving-patterns/longestSubstr-v2.ts[]| 1 | index - beginning of substring + 1 (to include current in count). |
| 2 | Store the index of the next char so as to not double-count. |
Again, the solution from the instructor is more elegant and concise than mine 🥲.